Document Reference: TN201009006 - Rev: 4.14 - Last Update: 14-11-2020 03:57 GMT - Downloaded: 28-Apr-2024 03:39 GMT
A standard XOR (Exclusive-OR) gate is a logic gate with two or more inputs and one output. An odd number of inputs states must be high to produce a high output.
XOR Gate Symbols
The inputs (A, B) of an XOR gate are on the left, and the output (X) is on the right of the logic XOR gate symbol.
| Distinctive Shape | Rectangular Shape | DIN Shape (Historic) |
|---|---|---|
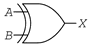 | 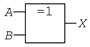 | 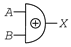 |
XOR Gate Truth Tables
Truth Table for XOR Gate with 2 Inputs
A | B | X |
|---|---|---|
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Truth Table for XOR Gate with 3 Inputs
A | B | C | X |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
XOR Gate Test-It
To test the gate, click the switch symbols in the image below.



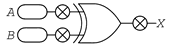
XOR Gate Logical Expressions
Word Equation
X = A XOR B
Boolean Algebra
In boolean algebra the plus sign with a circular border (⊕) stands for the XOR operation, e.g.:
X = A ⊕ B
Alternative notation: X = A ∨ B
A | B | X = A ⊕ B |
|---|---|---|
0 | 0 | X = 0 ⊕ 0 = 0 |
0 | 1 | X = 0 ⊕ 1 = 1 |
1 | 0 | X = 1 ⊕ 0 = 1 |
1 | 1 | X = 1 ⊕ 1 = 0 |
Note: X = A ⊕ B ⊕ C = (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)
A | B | C | X = (A ⊕ B) ⊕ C |
|---|---|---|---|
0 | 0 | 0 | X = (0 ⊕ 0) ⊕ 0 = 0 ⊕ 0 = 0 |
0 | 0 | 1 | X = (0 ⊕ 0) ⊕ 1 = 0 ⊕ 1 = 1 |
0 | 1 | 0 | X = (0 ⊕ 1) ⊕ 0 = 1 ⊕ 0 = 1 |
0 | 1 | 1 | X = (0 ⊕ 1) ⊕ 1 = 1 ⊕ 1 = 0 |
1 | 0 | 0 | X = (1 ⊕ 0) ⊕ 0 = 1 ⊕ 0 = 1 |
1 | 0 | 1 | X = (1 ⊕ 0) ⊕ 1 = 1 ⊕ 1 = 0 |
1 | 1 | 0 | X = (1 ⊕ 1) ⊕ 0 = 0 ⊕ 0 = 0 |
1 | 1 | 1 | X = (1 ⊕ 1) ⊕ 1 = 0 ⊕ 1 = 1 |

