The trapezoidal rule (aka trapezoid or trapezium rule) approximates the area under the graph of a function.
| We can use the trapeziodal rule for approximating definite integral | ∫ | b | f(x)dx |
| a |
Trapezium (British English) / Trapezoid (American English)
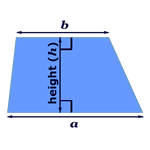
Area Formula For One Trapezoid (Trapezium)
| Area (A) | = | perpendicular height (h) | × | (a + b) |
| 2 |
We will use the notation below to demonstrate the trapezoid rule:
| A | = | h | (a + b) |
| 2 |
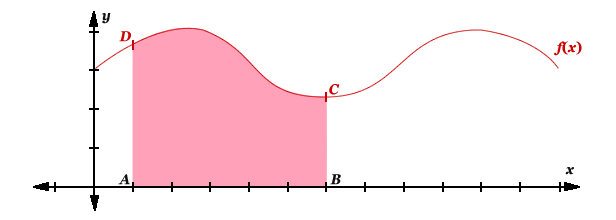
Graph Of A Function
Enclosed Area
Consider to calculate the coloured area under the graph shown below. The area is enclosed by the x-axis, the ordinate AD, the ordinate BC and the curve DC. We will divide the area in five segments and fill these segments with trapezoids of the same perpendicular height.
Fill With Trapezoids
To fill the area, turn a trapezoid by 90° and place it under the graph. Resize the parallel sides (a and b) to reach from the x-axis to the graph. Repeat to fill the required area.
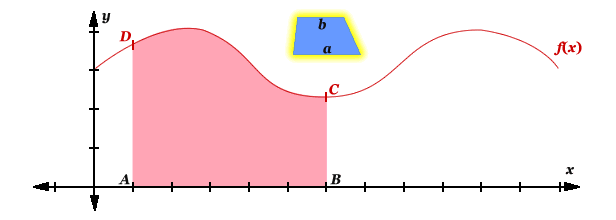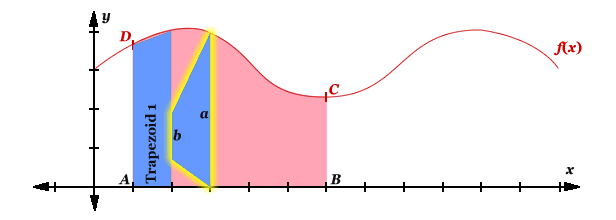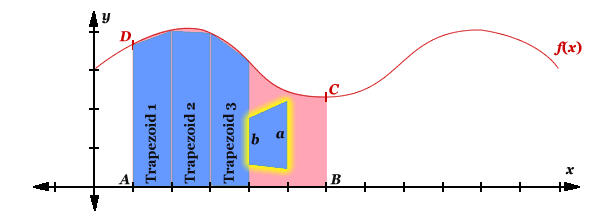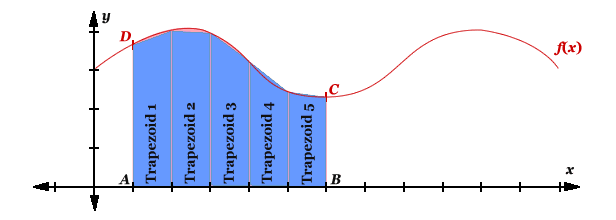
Dimensions
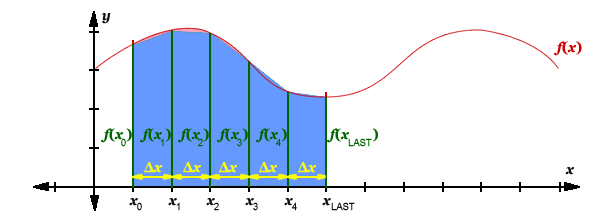
Once the area is filled with trapezoids, we can identify the dimensions of our trapezoids. The parallel sides of the trapezoids represents f(x0), f(x1), f(x2), f(x3), f(x4) and f(xLAST). The height of each trapezoid represents Δx. See graph below.
Formula
Area Formula For Trapezoids
We remember the area formula notation as stated at the beginning:
| A | = | h | (a + b) |
| 2 |
Now we apply it to the five trapezoids under our graph:
| Trapezoid 1 (A1) | = | Δx | [ f(x0) + f(x1) ] |
| 2 |
| Trapezoid 2 (A2) | = | Δx | [ f(x1) + f(x2) ] |
| 2 |
| Trapezoid 3 (A3) | = | Δx | [ f(x2) + f(x3) ] |
| 2 |
| Trapezoid 4 (A4) | = | Δx | [ f(x3) + f(x4) ] |
| 2 |
| Trapezoid 5 (A5) | = | Δx | [ f(x4) + f(xLAST) ] |
| 2 |
Sum Of All Trapezoids
Add all trapezoid areas to approximate the coloured area under the graph.
| Area | ≈ | A1 + A2 + A3 + A4 + A5 |
| Area | ≈ | Δx | [f(x0)+f(x1)] | + | Δx | [f(x1)+f(x2)] | + | Δx | [f(x2)+f(x3)] | + | Δx | [f(x3)+f(x4)] | + | Δx | [f(x4)+f(xLAST)] |
| 2 | 2 | 2 | 2 | 2 |
Simplify above formula:
| Area | ≈ | Δx | [f(x0) + 2f(x1) + 2f(x2) + 2f(x3) + 2f(x4) + f(xLAST)] |
| 2 |
| Area | ≈ | Δx | [f(x0) + f(xLAST) + 2 × (f(x1) + f(x2) + f(x3) + f(x4))] |
| 2 |
Now we can generalize this formula to obtain the final trapezoidal rule.
Trapezoidal Rule
And finally the formulas for the trapezoidal rule. The count of trapezoids used equals n. See also the alternative notation.
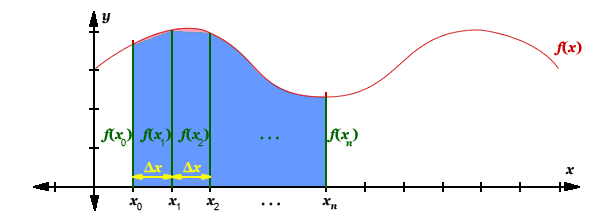
| ∫ | b | f(x)dx | ≈ | Δx | [f(x0) + f(xn) + 2(f(x1) + f(x2) + ... + f(xn-1))] | Δx | = | b − a | |
| a | 2 | n |
Alternative notation:
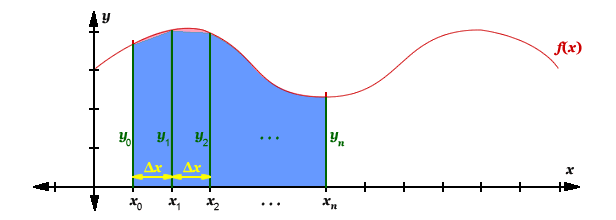
| ∫ | b | f(x)dx | ≈ | Δx | [y0 + yn + 2(y1 + y2 + ... + yn-1)] | Δx | = | b − a | |
| a | 2 | n |
Identifying Δx
Δx determines the height of our trapezoids and can be calculated by dividing the range by the number of chosen trapezoids n. The range can be calculated by subtracting the lower limit a from the upper limit b. The greater the number of trapezoids n, the closer the approximation.
| Δx | = | b − a |
| n |

