Real numbers are the type of number that we normally use in our day-to-day activities. Their value represent any quantity along a number line and their size can be compared.
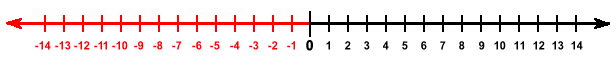
Example of a real number line displaying numbers from -14 to 14 only.
We use the letter ℝ (double-struck capital R) to label the real number set.
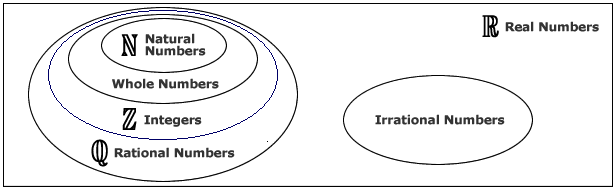
Real numbers include natural numbers, whole numbers, integers, rational numbers (fractions/decimal numbers) and irrational numbers.
Natural Numbers (Counting Numbers)
Natural numbers have no decimal places, have no fractional parts and can not be negative. They are the numbers that we use for counting (1, 2, 3 ...) and ordering (1st, 2nd, 3rd ...). The natural number set is infinite (never-ending).
We use the letter ℕ (double-struck capital N) to label the natural number set: ℕ = {1, 2, 3, 4, 5, 6 ... }.

Example of a natural number line displaying numbers from 1 to 31 only.
Whole Numbers
Whole numbers are the same as natural numbers, including the 0.

Example of a whole number line displaying numbers from 0 to 30 only.
Natural vs Whole Numbers
Above definition of natural and whole numbers is a traditional approach and you will find some publications stating that natural numbers are the same as whole numbers, e.g. natural numbers include the 0 as well. This is something we should be aware of but doesn't need to concern us at this time.
Integers
Integers have no decimal places and have no fractional parts. Unlike natural numbers, integer include the number 0 and can be positive or negative.
We use the letter ℤ (double-struck capital Z) to label the integer number set: ℤ = {... -3, -2, -1, 0, 1, 2, 3 ...}.
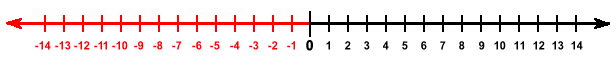
Example of a integer number line displaying numbers from -14 to 14. This representation is the same as the one above for our real number line. Remember, the difference is that integer numbers do not have decimal places or fractional parts.
Decimal Numbers (Base Ten)
Decimal numbers include a decimal point and one or more digits to the right of this decimal point. The part to the left of the decimal point is called integer part and the part to the right of the decimal point is called the fractional part.

Terminating Decimal Numbers
A decimal number that ends is a terminating decimal number. A number such as 1.25 is called terminating decimal number because it ends after 2 decimal places.
Recurring Decimal Numbers (Repeating Decimal)
Converting the fraction 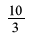 to decimal will result to 3.333333..., which contains an infinite number of decimal places and is therefore called a recurring decimal number.
to decimal will result to 3.333333..., which contains an infinite number of decimal places and is therefore called a recurring decimal number.
A dot above the first and last repeating digit or a bar above the repeating digit(s) can be used to represent recurring decimal numbers, e.g. 3.333333... = 3.3.
Rational Numbers (Fractions)
Rational numbers are numbers that can be represented as the ratio of two integers.
We use the letter ℚ (double-struck capital Q) to label the rational number set: 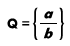 .
.
The numerator a and the denominator b are integers 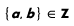 and
and b is not 0 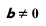 .
.
Most numbers that we use in our daily life are rational numbers, e.g. the integer number 1 and the recurring decimal number 3.3 are rational numbers as these number can be represented as a ratio of two integers:
| 1 | = | 2 | 3.3 | = | 10 | ||
| 2 | 3 |
Irrational Numbers
Irrational numbers are numbers that can not be converted to a fraction and are therefore non-terminating and non-recurring decimals.
The constant π (pi) and √2 are examples of the best known irrational numbers.

